¶ PCM 格式
计算机处理数据一般使用 PCM(Pulse-Code Modulation) 格式数据,其主要思想为通过方波近似替代原始音频波形。
¶ PCM 格式数据
假设原始信号(或称模拟信号)为 则 PCM 的数据一般经由如下步骤生成:
¶ 1. 采样
采样是将原始数据沿时间离散化的过程,形式化的说,即为从原始信号 生成离散数据(或称数字信号) 的过程
其主要实现方式为等距采样,步骤如下:
- 设定采样率 ,表示 内采样的点的个数单位为 Hz
- 在给定时间区间 内,步长为 ,对所有 计算得到 的离散数据为
其过程可以表述为下图:
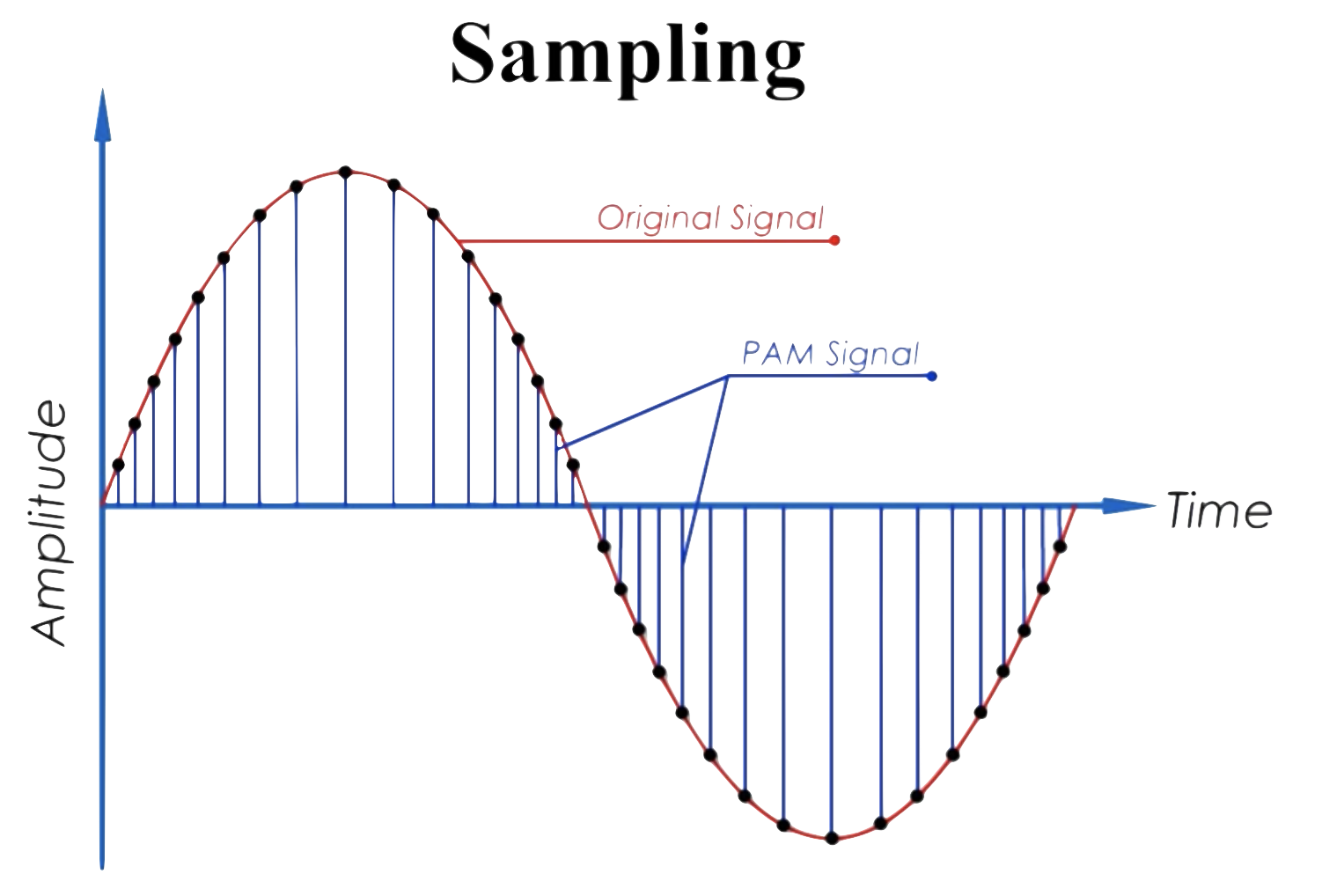
不难发现,在这一过程中,采样率的高低将会决定采样本身的精细程度,进而影响信号本身的信息是否丢失。但采样率并非越高越好,过高的采样率会导致冗余数据,过低的采样率会导致信号本身的失真(见 Downsample 失真),具体来说我们有如下定理给出信号采样过程中“最优”的采样率:
奈奎斯特-香农采样定理,如信号 存在最高频率 ,则采样率至少需要为 才能离散信号中完全重建原始信号
其中 称作奈奎斯特频率。结合初中物理可知,人耳最高可以听到的频率为 kHz, 因此理论上采样率设置在 kHz 便以足够。但在实际编曲过程中,为了留有一定的冗余的处理空间,一般选取 kHz 或 kHz。
¶ 2. 量化
通过采样步骤得到数字信号 后,因为计算机不能储存无限精度的数字,所以在采样之后需要对值域进行离散化。
其具体实现方式如下
- 将数字信号标准化,,此时
- 选取位深 , 单位为 bit
- 对于每一个 ,找到 满足 最小,得到
其过程可视化如下(以 8-bit 位深为例)
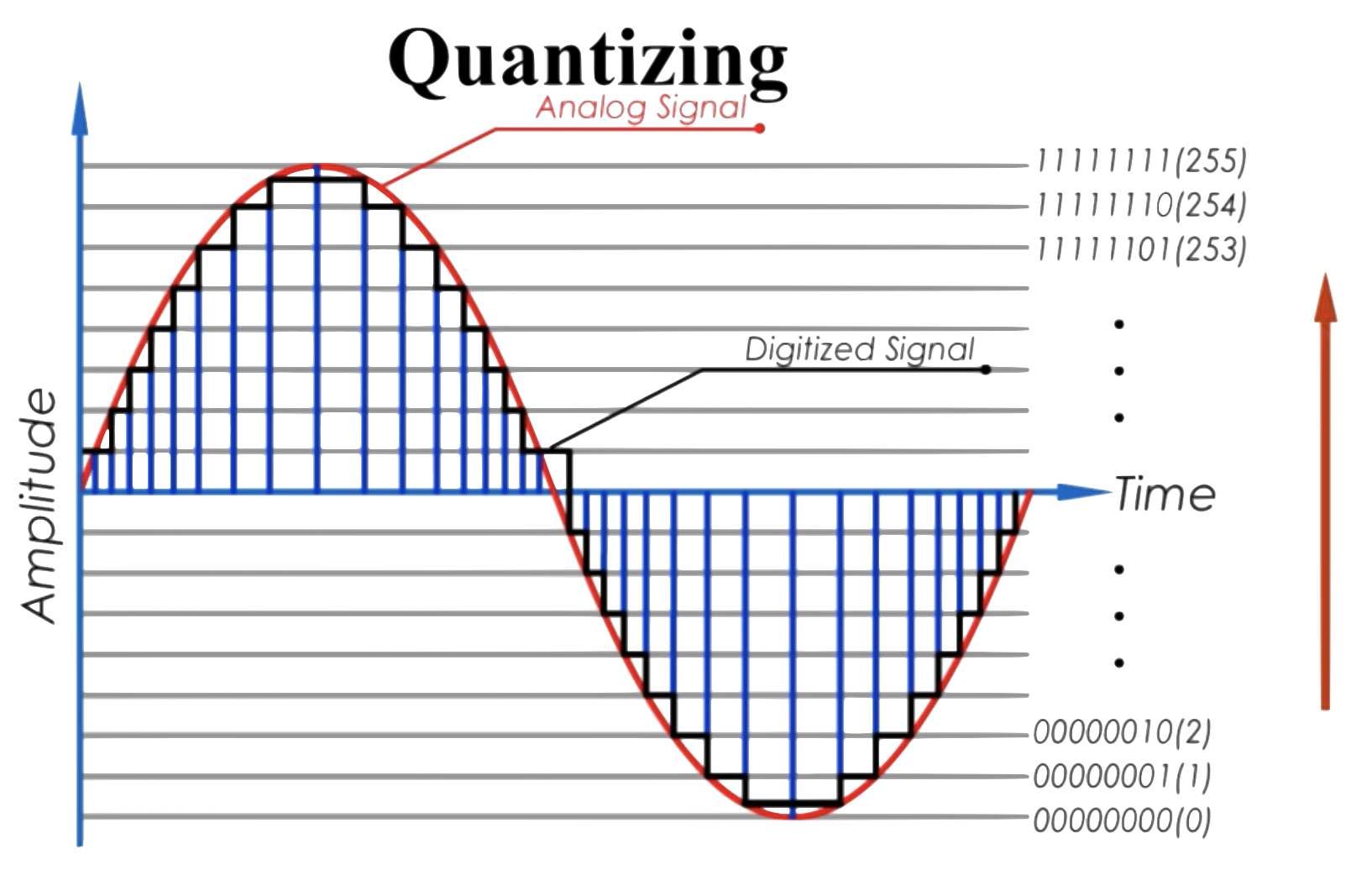
编曲实践中一般使用 bit 作为位深
¶ 3. 编码
将由量化过程得到的最终信号 通过一系列方式编码得到最终输出为文件/可解析格式。如 WAV 编码(直接存储 PCM)FLAC 编码(无损压缩 WAV),MP3 编码(有损压缩编码)。